南京大学计算机系统基础实验 ICSPA（2023）PA 1 阶段 2
表达式求值
表达式求值的作用是让我们能够在 NEMU 里进行数学运算，为后续的监视点功能提供基础。
词法分析
根据讲义的描述，NEMU 会将我们输入的表达式分解为一个个的 token，然后识别每个 token 的类型并存储下来，如果是数值还需要把 token 的具体内容也存下来。这样计算机就能够理解我们输入的内容。后面再根据 token 来生成表达式树，从而进行递归求值，这一过程就是 BNF。
我们需要实现的，就是编写 token 的识别规则。
我们可以根据讲义找到 make_token() 函数，在该函数的函数体中，最先可以找到一个 TODO：
分析代码可以发现，这里其实是匹配完 token 之后对 token 进行操作的地方（比如，如果 token 是数字则还需要把具体内容也存下来），并不是 token 匹配规则的地方。
我们现在需要做的是补充 token 的识别规则，应当在 rules[] 里实现。查看 rules[] 的定义就可以看到真正需要补充代码的地方：
.regex 的内容可以知道，.regex 应当是一个正则表达式的匹配规则。但是在 make_token() 中并没有发现任何地方使用 rules[] 来匹配 token，那么 NEMU 是怎么进行匹配的呢？
分析代码可知，在 NEMU 初始化的时候，会调用 init_regex() 来将我们在 rules[] 里编写的匹配规则进行处理，并将正则表达式初始化到 re[] 数组中，而 re[] 数组在 regexec() 中被作为参数传入，从而进行 token 的匹配。
因此，我们根据已有的格式，分别在上面提到的两个地方，将讲义中提到的
- 十进制整数
+,-,*,/(,)- 空格串(一个或多个空格)
的正则表达式匹配规则补充完成。
接下来，还需要在循环中将匹配到的 token 添加到 tokens[] 数组中，给接下来的环节使用。需要额外注意的是，TK_NUM 还需要将字符串的值复制到 tokens[].str 中；而 TK_NOTYPE 代表空格，其实可以直接忽略，不添加进去。
递归求值
接下来需要完成表达式的计算，从而实现 p 指令。递归求值可以用分治的思想来解决。
分治的思想是“将问题划分为完全相同但是规模更小的子问题”。在这里，我们将题目概括为求一个表达式的值，那么规模更小的问题就是求一个子表达式的值。我们从右到左遍历当前表达式的每一个 token，然后找到优先级最低的运算符，分别求出这个运算符左边和右边的“子表达式”的值，再将其进行运算就可以得出当前表达式的值。
我们平时进行运算的时候都是从优先级高的开始，为什么这里是从优先级低的开始呢？而且还是从右到左，也和平时从左到右不一样。这是因为我们进行的是递归求值，表达式最终会从递归最底部开始计算，然后将结果返回给上一层，上一层再开始计算。所以越深层应当是越先需要计算的运算符，也就是优先级越高的运算符。
整个递归求值的过程可以分成以下步骤：
- 判断表达式是否被括号包围。
- 从右到左找到优先级最低的第一个运算符（需要考虑括号）。
- 递归求得子表达式的值，计算当前表达式的值并返回。
利用递归分值的思想，按照讲义中说的方法写就好了，没有什么太多需要理解思考的地方。
其实现在不做的话，下一章也要做了。
实现方式是通过判断 - 符号之前的 token 是什么类型的，就可以判断当前 - 是什么类型了。
如何测试你的代码
讲义的方法是，先实现一个能够生成随机表达式的 gen-expr 程序，然后将生成的表达式直接写入一个 c 文件里赋值给一个变量，然后输出这个变量就好了。相当于是利用了 gcc 编译器的表达式求值的功能来为我们自己写的表达式求值进行验证。
重复运行 gen-expr，将其生成的表达式和表达式对应的值写入到一个文件中，再修改 NEMU，让其直接从该文件中读取表达式和值，然后调用 expr() 进行求值，并比较正确性。
从文件中读取有很多种方法，我使用的方法是直接用 Linux 的管道符 < 进行输入。找到 NEMU 编译生成的可执行文件后，手动运行，并使用管道符将 input 文件输入即可。这样的好处是不需要修改太多的代码。
运行代码就可以发现，如果出现了除 0 错误，编译器会报一个警告：
并且计算得到的值是 Nan，可以利用这个特征来进行过滤。
观察 gen_expr.c 的代码可以发现，其使用 fscanf() 来从进程中读取计算后的结果，而该函数的返回值和 scanf() 是一样的，返回成功读取的变量个数。利用这个就可以进行除 0 的过滤了：检测到成功读取的个数不为 0 就直接 continue。
'\n' 也读取进来，需要额外处理这种情况。我在验证的时候经常发现一个问题：如果表达式非常长，那么大概率我的表达式求值计算出来的数值和答案不一样。
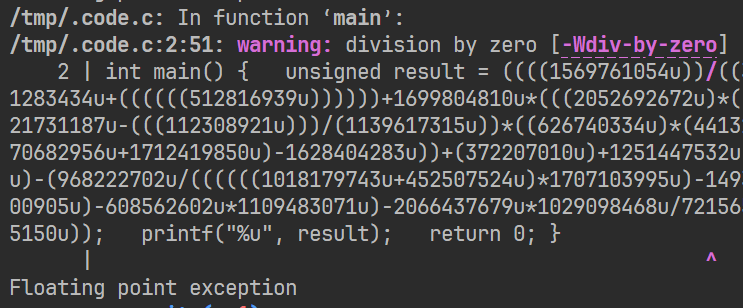
由于表达式过于长，手动计算过于复杂，故放弃。我想了很多可能的问题，结果也都不是。
我在尝试进行复现的时候，发现直接运行代码会导致栈溢出错误，我猜测可能是表达式过长导致 gcc 的编译器出现错误。
到此结束
PA 1 阶段 2 到此结束。